Dear Jianguo,
To render the Fermi surface correctly, it is essential to obtain energy values at all points on the 3D grid (kx, ky, kz). Without this, the isosurface cannot be rendered smoothly. The same requirement applies to the superconducting gap function to be visualized on the Fermi surface—it must be given at all points.
However, since EPW calculates the superconducting gap function only within the range of the fsthick window, rendering can fail, resulting in pixelated coloring, particularly when the grid points are coarse. To resolve this, the fsthick value must be increased or the kf grid refined. In your case, using a 36×36×36 grid, the resolution is too coarse, requiring a significantly larger fsthick. Even with a finer kf grid, such as 100×100×100, unnatural mottled patterns may still appear, which can be eliminated by further increasing the fsthick value.
In the calculations shown in [H. Mori
et al., PRB 110, 064505 (2024)], although the superconducting gap function converged at fsthick=0.3, a value of fsthick=0.5 was used to produce the clear and visually smooth plot of the gap function shown in Fig. 3. The image below shows the superconducting gap function on the Fermi surface with fsthick=0.3. You can see some small dots, which disappear when fsthick is increased to 0.5.
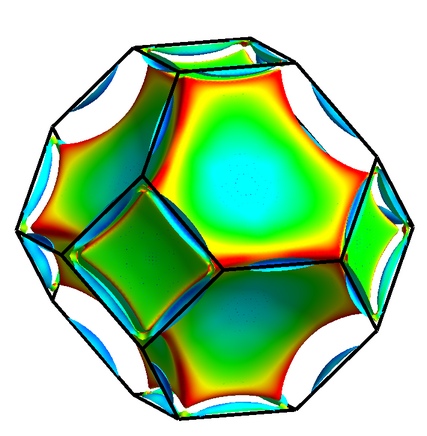
- tiny_dots.png (144.51 KiB) Viewed 19472 times
It is important to note that this issue is distinct from the convergence of the superconducting gap function or Tc. Even if the gap function at the Fermi energy are sufficiently converged with respect to the kf grid and fsthick, these parameters may still need to be increased solely to ensure proper rendering.
For reference, the file
prefix.imag_aniso_gap0_XXX.XX.frmsf contains the superconducting gap function at the smallest Matsubara frequency. It does not output results for analytic continuation to real frequencies, so it is not related to Padé approximant.
Best regards,
Hitoshi